Теорема 1. Пусть функция имеет в точке производные до п- го порядка включительно. Тогда для остаточного члена имеет место равенство. Прежде всего, заметим, что существование производных означает следующее: функция имеет производные до -го порядка в некоторой окрестности точки , и имеет производную п- го порядка в самой точке.

Конев В.В. Дифференцирование функций

Конев В. Дифференцирование функций. Разделы курса Примеры Калькулятор. Пределы Неопределенные интегралы Определенные интегралы Несобственные интегралы. Остаточный член в форме Коши.

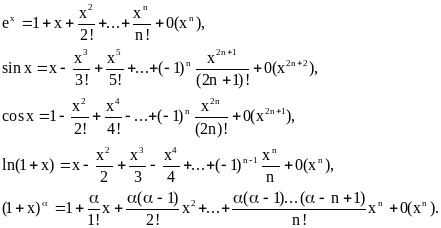
Регистрация Вход. Вопросы - лидеры. Помогите решить по однкнр срочно!!! Механика 1 ставка.

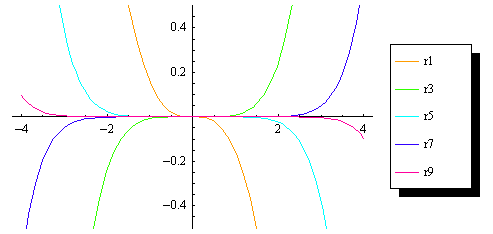
• §3. Формула Маклорена. Оценка Rn(X)
• Конев В. Дифференцирование функций.
• Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций.
• В этом году у меня больше часов на матанализ, поэтому удалось даже рассказать на практике про разные формы остаточного члена формулы Тейлора.
• Содержание
• Есть иные формулировки теоремы Тейлора, для которых остаточный член имеет несколько отличную форму. В приложениях формулу Тейлора используют следующим образом.
• Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля.
• Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде. Рассмотрим вспомогательную функцию.

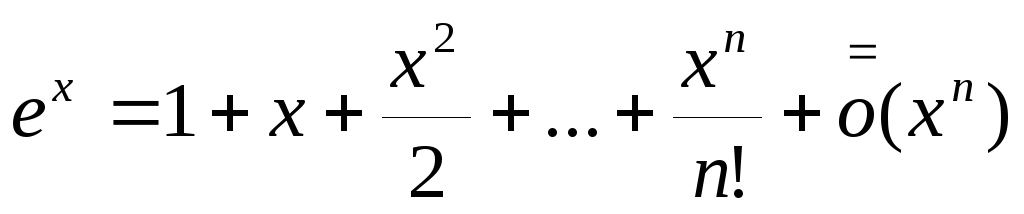
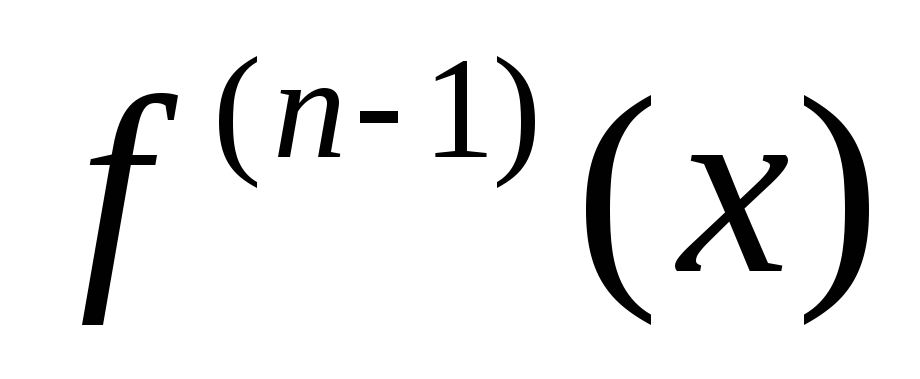
Список курсов ВМ. Остаточный член формулы Тейлора - Пусть функция имеет в точке производные всех порядков до -го включительно. Тогда для справедлива формула Тейлора :. Если отбросить остаточный член, то получится приближенная формула Тейлора. Приближенная формула позволяет заменять в различных математических расчетах аналитических и численных произвольную функцию ее многочленом Тейлора. Из формулы Тейлора видно, что чем точка ближе к точке , тем выше точность такой аппроксимации и эта точность растет с ростом степени многочлена.

Похожие статьи

• Секс куда вставлять член
• Вводить член во влагалище должна женщина
• Огромный член в жопу больно туб
• Видео девушки ласкающие член парня